Resources from: https://en.wikipedia.org/wiki/Proportional%E2%80%93integral%E2%80%93derivative_controller

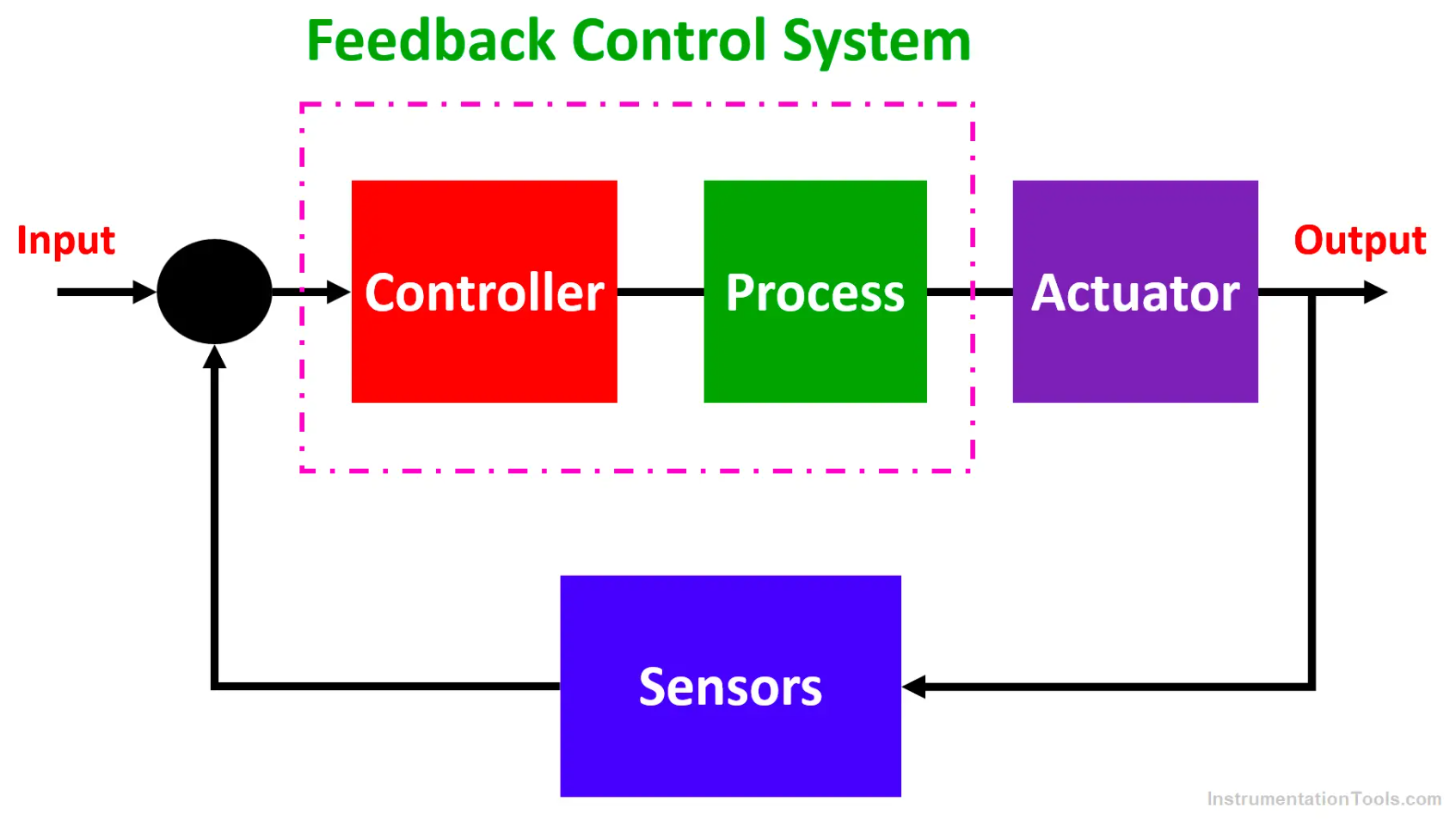
Feedback Control System

Operation

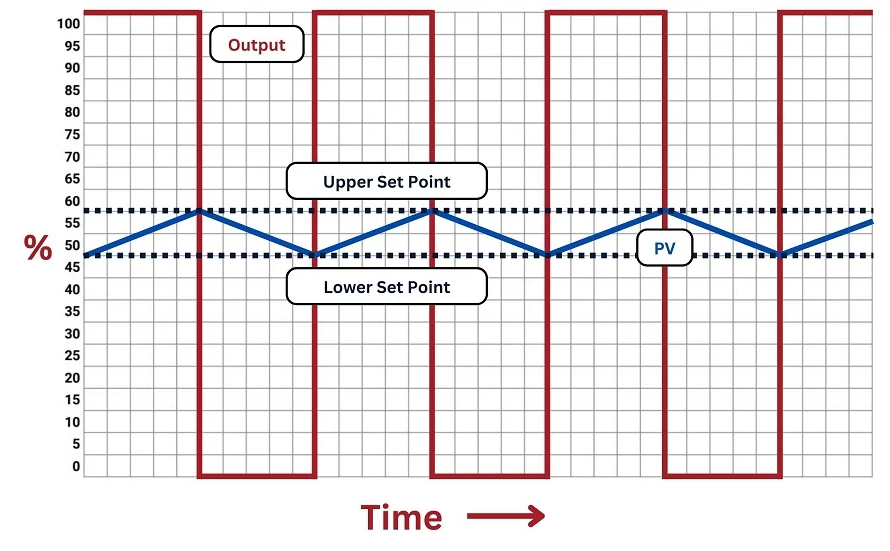
Types

Bang-Bang Controller

P Loop

PID

Take-Half Back

The PID

The PID control scheme is named after its three correcting terms: The proportional, integral, and derivative. terms are summed to calculate the output of the PID controller.

P Term (Proportional)

The proportional term produces an output value that is proportional to the current error value. The proportional response can be adjusted by multiplying the error by a constant Kp, called the proportional gain constant.

The proportional term is given by

In Code:

float Kp = 1.0;                 // Random Kp value

while (true) {                  // Loop infinitely
    float Pterm = error*Kp;     // Sum Error through time
}

I Term (Integral)

The contribution from the integral term is proportional to both the magnitude of the error and the duration of the error. The integral in a PID controller is the sum of the instantaneous error over time and gives the accumulated offset that should have been corrected previously. The accumulated error is then multiplied by the integral gain (Ki) and added to the controller output.

The integral term is given by

The integral may look/sound scary for those unfamiliar with calculus, but all it means is the SUM of the error over time. AKA just doing this a bunch:

In Code:

float Ki = 1.0;                 // Random Ki value

while (true) {                  // Loop infinitely
    float Integral += error;    // Sum Error through time
    float Iterm = Ki*Integral   // calculate the I term
}

D Term (Derivative)

The derivative of the process error is calculated by determining the slope of the error over time and multiplying this rate of change by the derivative gain Kd. The magnitude of the contribution of the derivative term to the overall control action is termed the derivative gain, Kd.

The derivative term is given by

Similarly with the D term as the I term, but all it means is the difference of the error over time.

In Code:

float Kd = 1.0;                                    // Random Kd value
float prevError = 0;                               // initalize previous error

while (true) {                                     // Loop infinitely
    float Dterm = Kd*(error - prevError);          // Sum Error through time
}

Typical PID response

Parameter	Rise Time	Overshoot	Settling Time	Steady-state error	Stability
Kp	Decrease	Increse	Small change	Decrease	Degrade
Ki	Decrease	Increase	Increase	Eliminate	Degrade
Kd	Minor Change	Decrease	Decrease	No effect in theory	Improve if Kd

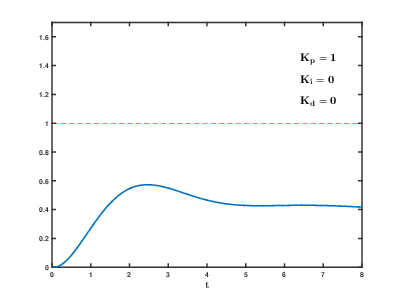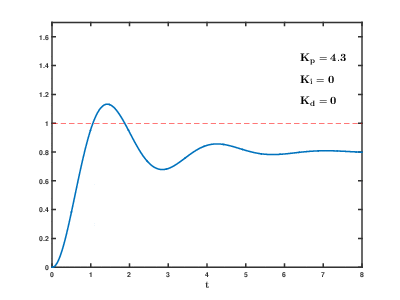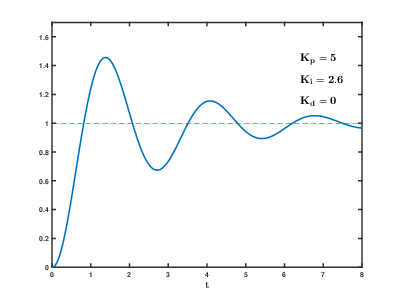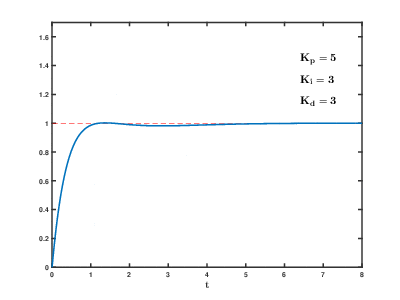
PID in Code

In Code:

float Kp = 1.0, Ki = 1.0, Kd = 1.0;                // Random Kp, Ki, and Kd coefficients
float prevError = 0;                               // initalize previous error

while (true) {                                     // Loop infinitely
    float Pterm = error*Kp;                        // Sum Error through time
    float Integral += error;                       // Sum Error through time
    float Iterm = Ki*Integral                      // calculate the I term
    float Dterm = Kd*(error - prevError);          // Sum Error through time

    float PIDout = Pterm + Iterm + Dterm;          // The PID response
}

Tuning Methods

Further Improvements

Integral Windup

Gain Scheduler

Feed-Forward System

Object Oriented PID's

Header File (.h):

class PID {
    // Private means that these variables/methods can only be accessed from the methods within the class itself
    private:                                      
        double Kp = 0.0, Ki = 0, Kd = 0.0;        // The P.I.D. gain coefficients
        double integral = 0.0, prevError = 0.0;   // integral, previous error (for "I" and "D" coeff.)
        double windup = 100.0;                    // the integral windup term - prevents the I response from building up too high.
        double maxPower = 100.0;                  // max output of the motors (typically 100%)
        double minPower = 0.0;                    // minimum output of the motors (you can't move a robot at 0% motor power after all!)

    // Public means that you can call/access everything in main.
    public:
        double Pterm = 0.0, Iterm = 0.0, Dterm = 0.0; // Initalizing external access variables
        double initI = 50.0;                          // The starting I sum term - lower it for the I to have less effect on the system
        
        PID(double kp, double ki, double kd);         // A constructor - this is how you specify creating the object

        double calculate ( double error );                   // calculate the PID response
        void reset( void );                                  // reset the integral and previous error
        void adjPID(double kP, double kI, double kD);        // adjust the objects PID gain terms
        void adjWindup( double wTerm = 100.0 );              // adjust the windup term (default to 100)
        void setVel( double toMinPower, double toMaxPower ); // set the maximum velocity of the response
};

Body File (.cpp):

// Constructor for Class definition
PID::PID(double kp, double ki, double kd) : Kp(kp), Ki(ki), Kd(kd) {}

// Calculate the PID response (expects an error input, in degrees or pct manuever)
double PID::calculate( double error ) {
  
  //                    {CODE GOES HERE}
  // Figure out how to write your own calculation here!

}

// Reset the PID internal variables
void PID::reset( void ){

  //                    {CODE GOES HERE}
  // Figure out how to write your own code here!

}

// Adjust the PID coefficients
void PID::adjPID(double kP, double kI, double kD){

  //                    {CODE GOES HERE}
  // Figure out how to write your own code here!
  
}

//adjust the windup behavior of the PID
void PID::adjWindup( double wTerm ) { 
    //{CODE GOES HERE} 
  }

//set the maximum and the minimum velocity output of the pid
void PID::setVel(double toMinPower, double toMaxPower){
  
  //                    {CODE GOES HERE}
  // Figure out how to write your own code here!
  
}